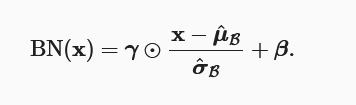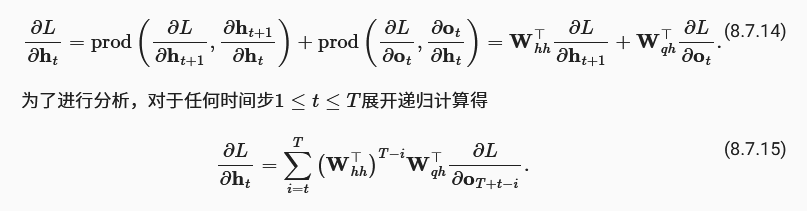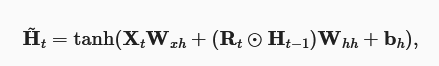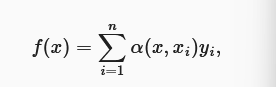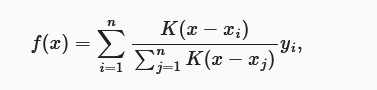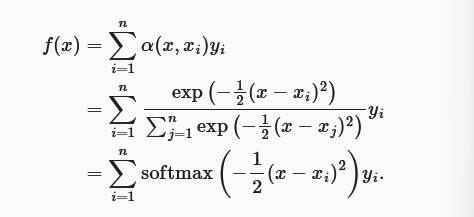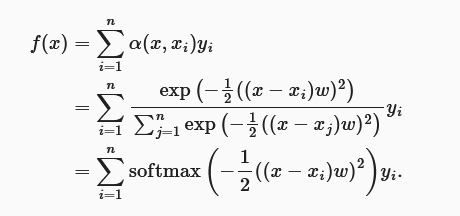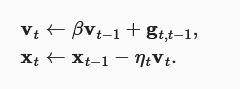『深度学习』动手学深度学习——阅读笔记2

❀目录❀

『深度学习』动手学深度学习——阅读笔记1

『深度学习』动手学深度学习——阅读笔记2

七. 现代神经网络

5. BN（批量标准化）

对于典型的多层感知机或卷积神经网络。当我们训练时，中间层中的变量（例如，多层感知机中的仿射变换输出）可能具有更广的变化范围：不论是沿着从输入到输出的层，跨同一层中的单元，或是随着时间的推移，模型参数的随着训练更新变幻莫测。 批量规范化的发明者非正式地假设，这些变量分布中的这种偏移可能会阻碍网络的收敛。

$ \gamma $ 和 $ \beta $ 都是可学习参数，分别用作对标准化后的值进行缩放(scale)和平移(shift)，提高网络的表达能力(不加此参数的话，中间层的输出将被限制在标准正态分布下)。随着网络的训练，网络会学到最合适的 $\gamma$ 和 $\beta$，最终中间层的输出将服从均值为 $\beta$，方差为 $\gamma^{2}$ 的正态分布。

对于卷积层而言，每个通道单独做批量规范化，每个通道都有自己的拉伸（scale）和偏移（shift）参数，这两个参数都是标量。

如何手写一个层（广播机制很重要，可以简化一些维度上的变化）：

class BatchNorm(nn.Module):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    # num_dims：2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var
        # 复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y
    
    def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
    if not torch.is_grad_enabled():
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。
            # 这里我们需要保持X的形状以便后面可以做广播运算
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # 训练模式下，用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 缩放和移位
    return Y, moving_mean.data, moving_var.data

深度学习的某些本质（误：

直观地说，批量规范化被认为可以使优化更加平滑。 然而，我们必须小心区分直觉和对我们观察到的现象的真实解释。 回想一下，我们甚至不知道简单的神经网络（多层感知机和传统的卷积神经网络）为什么如此有效。 即使在暂退法和权重衰减的情况下，它们仍然非常灵活，因此无法通过常规的学习理论泛化保证来解释它们是否能够泛化到看不见的数据。

在提出批量规范化的论文中，作者除了介绍了其应用，还解释了其原理：通过减少内部协变量偏移（internal covariate shift）。 据推测，作者所说的内部协变量转移类似于上述的投机直觉，即变量值的分布在训练过程中会发生变化。 然而，这种解释有两个问题： 1、这种偏移与严格定义的协变量偏移（covariate shift）非常不同，所以这个名字用词不当； 2、这种解释只提供了一种不明确的直觉，但留下了一个有待后续挖掘的问题：为什么这项技术如此有效？ 本书旨在传达实践者用来发展深层神经网络的直觉。 然而，重要的是将这些指导性直觉与既定的科学事实区分开来。 最终，当你掌握了这些方法，并开始撰写自己的研究论文时，你会希望清楚地区分技术和直觉。

随着批量规范化的普及，内部协变量偏移的解释反复出现在技术文献的辩论，特别是关于“如何展示机器学习研究”的更广泛的讨论中。 Ali Rahimi在接受2017年NeurIPS大会的“接受时间考验奖”（Test of Time Award）时发表了一篇令人难忘的演讲。他将“内部协变量转移”作为焦点，将现代深度学习的实践比作炼金术。 他对该示例进行了详细回顾 (Lipton and Steinhardt, 2018)，概述了机器学习中令人不安的趋势。 此外，一些作者对批量规范化的成功提出了另一种解释：在某些方面，批量规范化的表现出与原始论文 (Santurkar et al., 2018)中声称的行为是相反的。

然而，与机器学习文献中成千上万类似模糊的说法相比，内部协变量偏移没有更值得批评。 很可能，它作为这些辩论的焦点而产生共鸣，要归功于目标受众对它的广泛认可。 批量规范化已经被证明是一种不可或缺的方法。它适用于几乎所有图像分类器，并在学术界获得了数万引用。

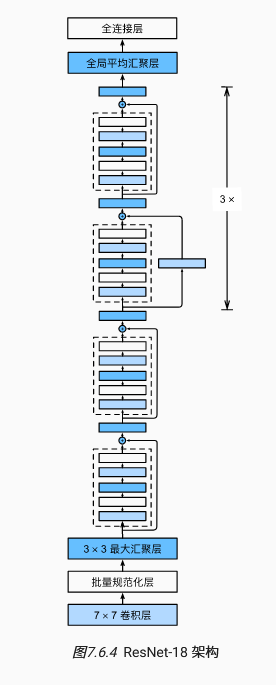
6. Resnet

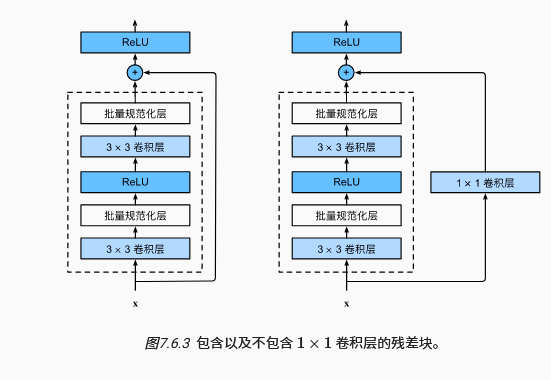
在每个Block的第一个残差块中，完成通道数翻倍与长宽减半的操作，在后续的残差块中，通道数和长宽均保持不变，第一个Block是例外。整个网络主体是多个Block，一个Block内部有多个残差块，一个残差块的内部如上图所示，分为两类。

• 学习嵌套函数（nested function）是训练神经网络的理想情况。在深层神经网络中，学习另一层作为恒等映射（identity function）较容易（尽管这是一个极端情况）。

• 残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零。

• 利用残差块（residual blocks）可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播。

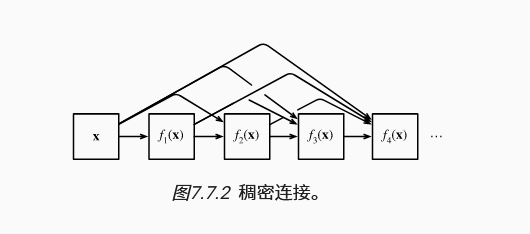
7. DenseNet

ResNet将f分解为两部分：一个简单的线性项和一个复杂的非线性项。 那么再向前拓展一步，如果我们想将f拓展成超过两部分的信息呢？ 一种方案便是DenseNet。

这样会导致通道数极多，每层稠密连接块后，需要过渡层来减少通道数并减半长与宽。

8. 总结

将 Conv - BN - ReLu 优化为 BN - ReLu - Conv - ... - Pool。

长宽通过Conv的stride / Pool (Pool甚至都用的少，或者说几乎不放在堆叠块内使用)调整，通道通过 Conv 调。

Pool用到的地方：

1. 最后的自适应全局池化
2. 最开始的浅层特征降采样

八. 循环网络

简言之，如果说卷积神经网络可以有效地处理空间信息， 那么本章的循环神经网络（recurrent neural network，RNN）则可以更好地处理序列信息。 循环神经网络通过引入状态变量存储过去的信息和当前的输入，从而可以确定当前的输出。

1. 序列模型

1.1 策略

两种策略，我们认为预测一个时间点上的数据，不需要以往全部时间点的数据，而只需要一个长度的时间跨度。

1. 自回归模型：同全连接层
2. 隐式自回归模型：保留一些对过去观测的总结$h_t$, 并且随时间步更新$h_t$。

事实上，如果基于一个马尔可夫模型， 我们还可以得到一个反向的条件概率分布。 然而，在许多情况下，数据存在一个自然的方向，即在时间上是前进的。 很明显，未来的事件不能影响过去。 因此，如果我们改变，可能会影响未来发生的事情，但不能反过来。 也就是说，如果我们改变，基于过去事件得到的分布不会改变。 因此，解释应该比解释更容易。

1.2 k步预测

模型预测下一个时间步的能力， 也就是单步预测（one-step-ahead prediction）。

k步预测即必须使用我们自己的预测（而不是原始数据）来进行多步预测，这一定会导致更大的偏差。

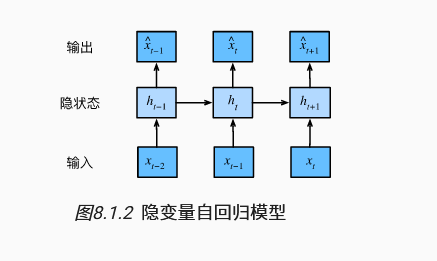
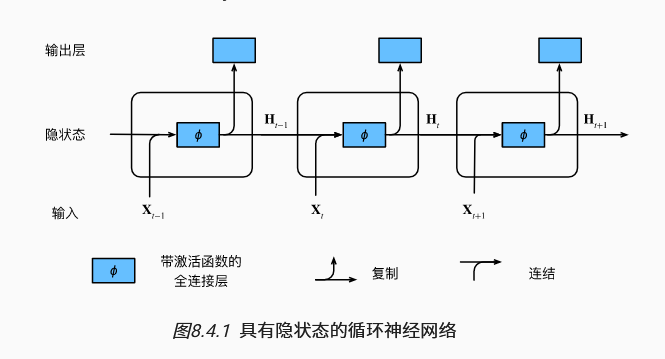
2. 有隐状态的循环神经网络

在循环神经网络（RNN）中，隐状态的概念是关键。假设我们有一个时间步长的输入序列 $X_t$，每个时间步对应于输入当前时间的样本。为了捕捉时间序列的依赖关系，循环神经网络会保留前一个时间步的 隐状态 $\mathbf{H}_{t-1}$，并通过权重矩阵 $W_{hh}$ 与当前输入 $\mathbf{X}_t$ 结合，计算出当前时间步的隐状态 $\mathbf{H}_t$：

$$\mathbf{H}_t = \phi(\mathbf{X}_t W_{zh} + \mathbf{H}_{t-1} W_{hh} + \mathbf{b}_h)$$

其中，$\phi$ 是激活函数，通常为 $\tanh$ 或 $\sigma$。

与传统神经网络不同，RNN 会通过这种递归的方式将前一时间步的隐状态与当前输入结合，从而捕捉序列中的依赖关系。这种机制使得网络能够记住之前时间步的信息，被称为 循环（recurrent）。因此，基于这种隐状态计算的网络称为 循环神经网络（Recurrent Neural Network, RNN）。

最后，输出层依赖于当前时间步的隐状态与权重矩阵 $W_{hq}$ 计算得出：

$$\mathbf{O}_t = \mathbf{H}_t W_{hq} + \mathbf{b}_q$$

RNN 的参数包括隐状态的权重 $W_{hh}$、输入的权重 $W_{zh}$、输出的权重 $W_{hq}$、以及对应的偏置项。尽管这些参数在每个时间步中保持不变，但 RNN 通过将隐状态递归地传递给下一个时间步，能够捕捉到时间序列中的长期依赖关系。

总结下核心思想：把每个时间点的特征打包，依次排队送入模型中，因此这个模型不需要处理时间维度，只需要每次更新内部隐藏状态即可，因此参数开销不会随着时间步的增加而增加，但运行时间开销会随着时间步的增加而增加。

3. 梯度裁剪策略

由于隐藏状态的持续更新，导致梯度反向传播时，在计算隐藏状态中间值的梯度时，由于复合函数求导，出现了矩阵大量连乘的情况，可能出现梯度消失或梯度爆炸。

解决方法有三：

• 截断时间步

• 随机截断

• 梯度裁剪

$$\mathbf{g} \leftarrow \min\left(1, \frac{\theta}{\|\mathbf{g}\|}\right) \mathbf{g}.$$

其中梯度裁剪使用较多，其核心思想即将梯度$g$投影回给定半径的球来裁剪梯度，如此可以缓解梯度爆炸，却无法缓解梯度消失。torch在实现该方法时，还会随时储存中间变量的梯度，以便重复使用，避免冗余计算。

九. 现代循环神经网络

上述循环神经网络存在问题：记忆遗忘，即早期记忆会随着迭代而消失，然而早期记忆可能很重要；一些记忆是无用的，不应该保留无用记忆等等。现代循环神经网络致力于解决这些问题。

1. 门控循环

1.1 重置门

重置门更新门皆有一组新的参数训练而成，仍然与时间步无关。

重置门控制来减少以往状态的影响，值越大代表越受过往影响，而值等于0时相当于抛弃了状态，与MLP无异。得到的结果成为候选隐状态。

1.2 更新门

更新门控制候选隐状态和上一步隐状态的比例，即当前的隐状态在多大程度上来自旧的状态和新的候选状态。

例如，如果整个子序列的所有时间步的更新门都接近于1， 则无论序列的长度如何，在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。

门控循环单元具有以下两个显著特征：

• 重置门有助于捕获序列中的短期依赖关系；
• 更新门有助于捕获序列中的长期依赖关系。

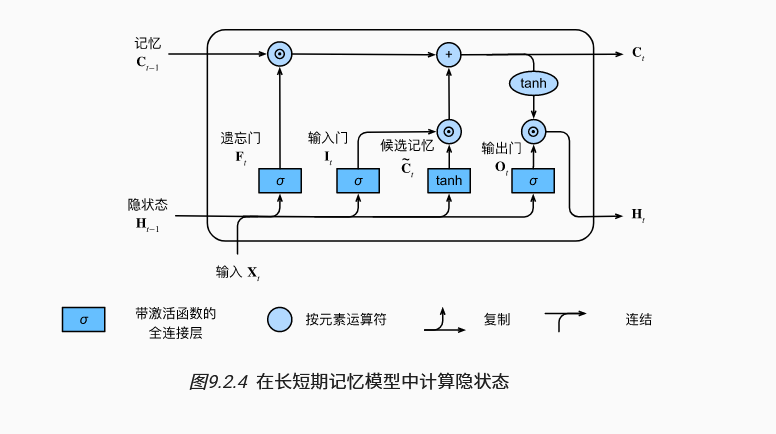
2. LSTM

与门控网络整体结构类似。

输入门，遗忘门，输出门：

长短期记忆网络是典型的具有重要状态控制的隐变量自回归模型。 多年来已经提出了其许多变体，例如，多层、残差连接、不同类型的正则化。 然而，由于序列的长距离依赖性，训练长短期记忆网络 和其他序列模型（例如门控循环单元）的成本是相当高的。

• 长短期记忆网络有三种类型的门：输入门、遗忘门和输出门。
• 长短期记忆网络的隐藏层输出包括“隐状态”和“记忆元”。只有隐状态会传递到输出层，而记忆元完全属于内部信息。
• 长短期记忆网络可以缓解梯度消失和梯度爆炸。

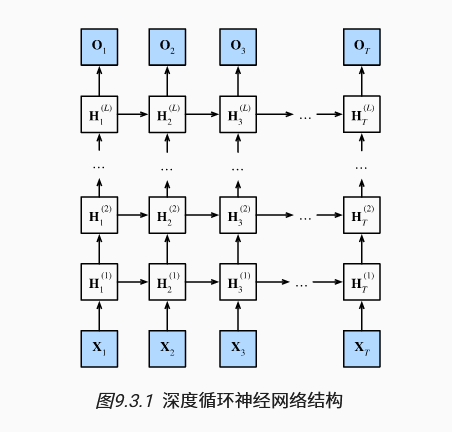
3. 深层循环网络

多个隐藏层叠加起来，可以产生更加灵活的机制，但是深度循环神经网络需要大量的调参（如学习率和修剪） 来确保合适的收敛，模型的初始化也需要谨慎。

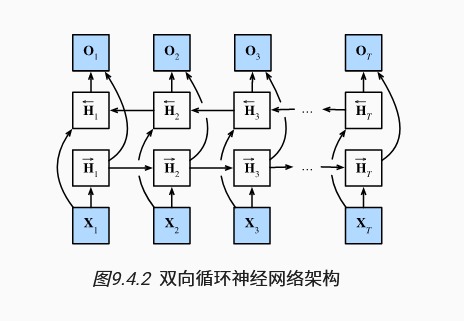
4. 双向LSTM

模型具备前瞻能力，更好的在当前时间步同时关注上文与下文。双向循环神经网络（bidirectional RNNs） 添加了反向传递信息的隐藏层，以便更灵活地处理此类信息。

双向的隐藏层各自独立，参数也独立互不影响，结果汇聚到输出层，在不考虑输出层的情况下，输出的神经元个数是隐藏层神经元个数乘以2。

双向层效果不好，使用在实践中非常少，并且仅仅应用于部分场合。 例如，填充缺失的单词、词元注释（例如，用于命名实体识别） 以及作为序列处理流水线中的一个步骤对序列进行编码（例如，用于机器翻译）。

5. Encoder-Decoder

• 根据“编码器-解码器”架构的设计， 我们可以使用两个循环神经网络来设计一个序列到序列学习的模型。

• 在实现编码器和解码器时，我们可以使用多层循环神经网络。

• 我们可以使用遮蔽来过滤不相关的计算，例如在计算损失时。

• 在”编码器－解码器”训练中，强制教学方法将原始输出序列（而非预测结果）输入解码器。

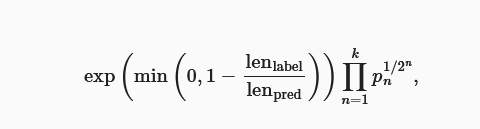
• BLEU是一种常用的评估方法，它通过测量预测序列和标签序列之间的n元语法的匹配度来评估预测。

十. 注意力机制

1. 基本原理

“是否包含自主性提示”将注意力机制与全连接层或汇聚层区别开来。自主性提示被称为查询（query）。 给定任何查询，注意力机制通过注意力汇聚（attention pooling） 将选择引导至感官输入（sensory inputs，例如中间特征表示）。 在注意力机制中，这些感官输入被称为值（value）。 更通俗的解释，每个值都与一个键（key）配对， 这可以想象为感官输入的非自主提示，可以通过设计注意力汇聚的方式， 便于给定的查询（自主性提示）与键（非自主性提示）进行匹配， 这将引导得出最匹配的值（感官输入）。

精简而言：注意力机制即找到一种计算方式，按一定的权重将不同的值汇聚起来，权重是由当前查询和各个键之间的某种相似度得到的，而权重之和应为1。

一个通用的计算公式如下，$x$为查村，$x_i$为键，$y_i$为对应的值

2. Nadaraya-Watson核回归

无参数形式

进一步化简为：

没有可学习的参数，仅仅是当键和查询越接近时，分配到的注意力权重便会越多。

有参数形式：只有一个可学习参数。

3. 注意力评分函数

3.1 掩蔽softmax

seq2seq的关键，Transformer解码器的核心机制。有些词元是填充词，在计算softmax时需要被忽略，为了仅将有意义的词元作为值来获取注意力汇聚， 可以指定一个有效序列长度（即有效词元的个数）， 以便在计算softmax时过滤掉超出指定范围的位置。

#@save
def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
                              value=-1e6)
        return nn.functional.softmax(X.reshape(shape), dim=-1)

3.2 加性自注意力

当查询和键是不同长度时，可以使用加性注意力，然而不同长度可以通过线性层转换，一般不使用该方法。

3.3 缩放点积注意力

最经典的算法，Transformer的基础。

缩放的原因：假设查询和键都满足零均值和单位方差，那么点积过后均值仍为0，而方差为d，因此我们需要除以根号d来规范方差仍为单位方差。

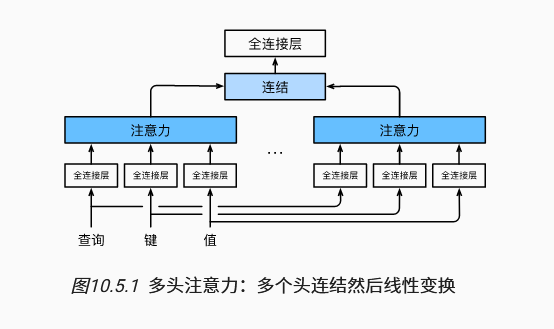
3.4 多头注意力

独立学习得到的组不同的 线性投影（linear projections）来变换查询、键和值。 然后，这组变换后的查询、键和值将并行地送到注意力汇聚中。 最后，将这个注意力汇聚的输出拼接在一起， 并且通过另一个可以学习的线性投影进行变换， 以产生最终输出。

每个头可能会关注输入的不同部分，可以学习到输入不同角度的特征。

我们通常设置各头的特征维度均相同，可以通过并行化计算的方法来简化编程和计算。比如将多个线性层矩阵合并计算，具体请参考Transformer的源码实现。

def predict_seq2seq(net, src_sentence, src_vocab, tgt_vocab, num_steps,
                    device, save_attention_weights=False):
    """序列到序列模型的预测"""
    src_tokens = src_vocab[src_sentence.lower().split(' ')] + [
        src_vocab['<eos>']]
    enc_valid_len = np.array([len(src_tokens)], ctx=device) # 计算实际长度！！
    src_tokens = d2l.truncate_pad(src_tokens, num_steps, src_vocab['<pad>'])
    # 添加批量轴
    enc_X = np.expand_dims(np.array(src_tokens, ctx=device), axis=0)
    enc_outputs = net.encoder(enc_X, enc_valid_len)
    dec_state = net.decoder.init_state(enc_outputs, enc_valid_len) # 在这步填充进解码器中，方便后续在attention中实现softmax掩码！！
    # 添加批量轴
    dec_X = np.expand_dims(np.array([tgt_vocab['<bos>']], ctx=device),
                           axis=0)
    output_seq, attention_weight_seq = [], []
    for _ in range(num_steps):
        Y, dec_state = net.decoder(dec_X, dec_state)
        # 我们使用具有预测最高可能性的词元，作为解码器在下一时间步的输入
        dec_X = Y.argmax(axis=2)
        pred = dec_X.squeeze(axis=0).astype('int32').item()
        # 保存注意力权重（稍后讨论）
        if save_attention_weights:
            attention_weight_seq.append(net.decoder.attention_weights)
        # 一旦序列结束词元被预测，输出序列的生成就完成了
        if pred == tgt_vocab['<eos>']:
            break
        output_seq.append(pred)
    return ' '.join(tgt_vocab.to_tokens(output_seq)), attention_weight_seq

3.5 自注意力，位置编码，Transformer

自注意力：

自注意力即kqv来自同一组输入，目前大多模型均使用自注意力机制。

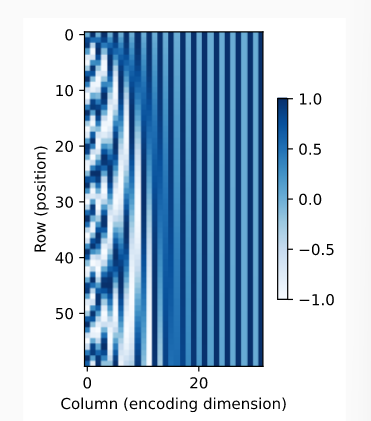
位置编码

由于Attention中不考虑位置因素，我们需要手动加上位置编码，一种经典的三角函数编码如下所示：

此函数为在时间维度上呈周期性波动的三角函数，且随着列数越靠后，周期越大。目前通常使用这种编码及其变种，如旋转位置编码（RoPE），相对位置编码等。

Transformer:

• Transformer是编码器－解码器架构的一个实践，尽管在实际情况中编码器或解码器可以单独使用。
• 在Transformer中，多头自注意力用于表示输入序列和输出序列，不过解码器必须通过掩蔽机制来保留自回归属性。
• Transformer中的残差连接和层规范化是训练非常深度模型的重要工具。
• Transformer模型中基于位置的前馈网络使用同一个多层感知机，作用是对所有序列位置的表示进行转换。

十一. 优化算法

本部分涉及凸优化理论，笔者数学基础目前有限，待进一步学习后尝试继续完善此节。

凸优化问题有助于分析算法的特点。 毕竟对大多数非凸问题来说，获得有意义的理论保证很难，但是直觉和洞察往往会延续。

1. 优化算法基础

小批量随机梯度下降：小批量指每次batch_size个样本同时计算，可以更好的利用向量化特性加速运算，随机指在样本中随机取出，这样可以对梯度有异常扰动，更适合收敛到最优解。

• 由于减少了深度学习框架的额外开销，使用更好的内存定位以及CPU和GPU上的缓存，向量化使代码更加高效。
• 随机梯度下降的“统计效率”与大批量一次处理数据的“计算效率”之间存在权衡。小批量随机梯度下降提供了两全其美的答案：计算和统计效率。
• 在小批量随机梯度下降中，我们处理通过训练数据的随机排列获得的批量数据（即每个观测值只处理一次，但按随机顺序），平均梯度的方法也减小了方差。
• 在训练期间降低学习率有助于训练。
• 一般来说，小批量随机梯度下降比随机梯度下降和梯度下降的速度快，收敛风险较小。

2. 动量法

核心为引入动量机制，可类比数学中的滑动均值的概念。

2.1 为何需要动量法

对于传统的梯度下降优化方法，存在显著的两难问题，例如两个自变量$x1, x2，y=x1+100*x2$，$x2$方向上的梯度比$x1$方向大得多，那么如果选择较小的学习率，则可以确保解不会在$x2$方向上发散，但要承受在$x1$方向的缓慢收敛；反之较大学习率，则在$x1$方向进展很快，但$x2$方向则会发散。

归根到底这是每个参数更新仅依赖于当前计算梯度和学习率导致的。

2.2 泄露平均值

上文说到，我们的随机梯度下降通过一小批样本取平均的方式减少了随机采样导致的方差。如果我们能够持续从方差减少中收益呢？我们采用泄露平均值（leaky average）取代梯度计算。这种方法也即动量法，公式如下。

我们动态维护每一个参数的过去平均梯度，并在参数更新时使用平均梯度而不是当前梯度进行更新，其中$\beta$为动量系数，一般取0.9/0.99，平均值初始化为$v_{0}=0$。

3. AdaGrad/RMSProp

此两种算法一脉相传。

3.1 稀疏特征的处理

稀疏特征即偶尔会出现的特征，比如AI相关材料中“深度学习”（假设编码为0011）总是要比”英雄联盟“（假设编码为1100）出现的更加频繁，而假设只有一个全连接层（四个参数，$w1,w2,w3,w4$），那么只有“英雄联盟”出现时，$w1,w2$才会得到有意义的更新。这会导致常见特征的参数会迅速收敛到最佳值，而对于“英雄联盟”的参数缺少足够的观测以确定其最佳值。换句话说，学习率要么对常见特征而言降低太慢，要么对稀疏特征而言降低太快。

因此需要设计一种方案来根据一个特征的出现频率来动态调整学习率，出现频率越高，则学习率更低，出现频率更低，则学习率更高。理想中可以设计一个特定特征次数出现的计数器$s(i, t)$，使得$\eta_i = \frac{\eta_0}{\sqrt{s(i, t) + c}}$。

3.2 AdaGrad

AdaGrad（自适应梯度下降）算法即设计了一种粗略计数器$s(i, t)$来统计频率，首先何为特征的出现频率，这是我们无法准确统计的，在这里，将参数先前的梯度平方和视作“频率”，进而使用$s(i, t+1) = s(i, t) + \left(\partial_i f(\mathbf{x})\right)^2$来计算频率进而调整学习率。归根到底即为每个参数进行独立的学习率调整，随着训练的进行，频繁更新的参数学习率会越来越低，而更新较少的参数会保持相对较大的学习率。

$$\begin{split}\begin{aligned} \mathbf{g}_t & = \partial_{\mathbf{w}} l(y_t, f(\mathbf{x}_t, \mathbf{w})), \\ \mathbf{s}_t & = \mathbf{s}_{t-1} + \mathbf{g}_t^2, \\ \mathbf{w}_t & = \mathbf{w}_{t-1} - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \cdot \mathbf{g}_t. \end{aligned}\end{split}$$

但其具备较大的局限性，诸如学习率趋于0等巨大问题，因此后续有很多工作皆是基于此继续调整算法。

3.3 RMSProp

AdaGrad算法的最大缺点在于其学习率按预定时间表$\mathcal{O}(t^{-\frac{1}{2}})$显著降低，即将梯度$g_t$的平方累加$\mathbf{s}_t = \mathbf{s}_{t-1} + \mathbf{g}_t^2$，如此没有约束力，$s_t$将持续增长，在算法收敛时呈线性递增。因此研究者借鉴了动量法中泄露平均值的思想，即令$\mathbf{s}_t \leftarrow \gamma \mathbf{s}_{t-1} + (1-\gamma) \mathbf{g}_t^2$，其余部分不变，便是RMSProp算法。在这种算法下，$s_t$权重为1的综合起历史时间步的梯度平方，使得参数学习率不会随时间收敛于0。

4. Adam

Adam算法是集大成者，将所有技术汇总到一起，是最常用的优化算法。我们直接介绍其算法原理——使用指数加权移动平均值估算梯度的动量（动量法）和二次矩（RMSProp算法）。

$$\begin{split}\begin{aligned} \mathbf{v}_t & \leftarrow \beta_1 \mathbf{v}_{t-1} + (1 - \beta_1) \mathbf{g}_t, \\ \mathbf{s}_t & \leftarrow \beta_2 \mathbf{s}_{t-1} + (1 - \beta_2) \mathbf{g}_t^2. \end{aligned}\end{split}$$

一般$\beta_{1} = 0.9, beta_{2} = 0.999$，方差估计移动远慢于动量估计的移动。接着，由于对$v,s$初始化为0，初始阶段存在较大偏差，因此需要在初始阶段作偏差校正：

$$\hat{\mathbf{v}}_t = \frac{\mathbf{v}_t}{1 - \beta_1^t} \text{ and } \hat{\mathbf{s}}_t = \frac{\mathbf{s}_t}{1 - \beta_2^t}$$

最后，更新梯度如下：

$$\mathbf{g}_t' = \frac{\eta \hat{\mathbf{v}}_t}{\sqrt{\hat{\mathbf{s}}_t} + \epsilon} \\ \mathbf{x}_t \leftarrow \mathbf{x}_{t-1} - \mathbf{g}_t'.$$

设计思路：$s,v$状态存储了参数梯度动量和规模，并可以通过稍微不同的初始化和更新条件来修正偏项；其次，两种算法组合简单，并且明确的学习率$\eta$使我们能够控制步长来解决收敛问题。

5. 学习率调度器

5.1 调度策略

首先我们具备明确的目标，即在训练过程中应逐步降低学习率，以便更好收敛或者说减小参数的固有方差。而降低学习率的策略分为多种，诸如线性调度策略，分段调度策略，余弦调度策略等。公式为余弦调度策略，较好理解，不过多赘述。

$$\eta_t = \eta_T + \frac{\eta_0 - \eta_T}{2} \left(1 + \cos(\pi t/T)\right)$$

5.2 预热策略

在某些情况下，初始化参数不足以得到良好的解。因此我们需要一种预热策略，在训练的早期阶段逐步提高学习率至最大值（为简单起见普遍使用线性递增策略），目的是在训练早期尽可能跳出局部最优区域而广泛寻找最优解，随后使用学习率调度器冷却直至结束，预热策略可以适用于任何调度器，一个可能的学习率变化图如下：

十二. 计算性能

参考OpenMLSYS学习笔记，在此不过多赘述。

十三. 计算机视觉

1. 转置卷积+全卷积网络

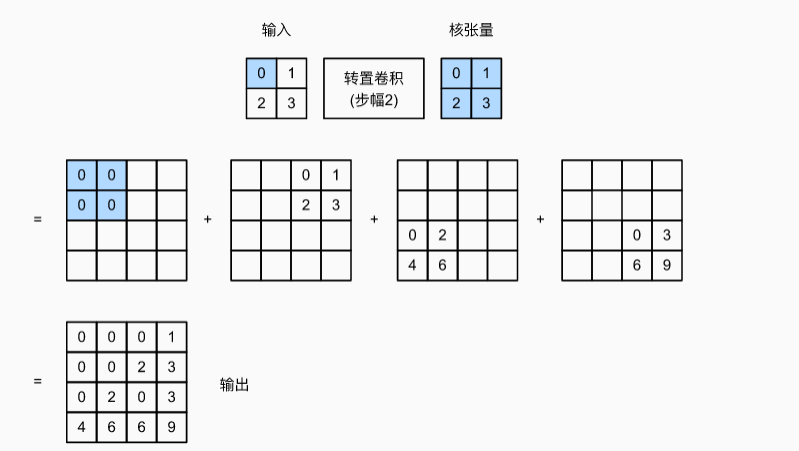
转置卷积：用于图像的上采样，类似普通卷积的逆操作，步长和填充应用在输出上，而不是像普通卷积一样应用在输入上，从数学分析：

• 步长=1，填充=0：此时 $输出的长宽 = 输入长宽 + 卷积核长宽 - 1$

• 步长=n：一般来说，核长宽为$n$且步长为$n$，填充为0时，可以令输出的长宽是输入长宽的n倍。

​ $输出长宽 = 步长 ( 输入长宽 - 1 ) + 卷积核长宽 - 填充 2$

• 与通过卷积核减少输入元素的常规卷积相反，转置卷积通过卷积核广播输入元素，从而产生形状大于输入的输出。

• 我们可以使用矩阵乘法来实现卷积。转置卷积层能够交换卷积层的正向传播函数和反向传播函数。

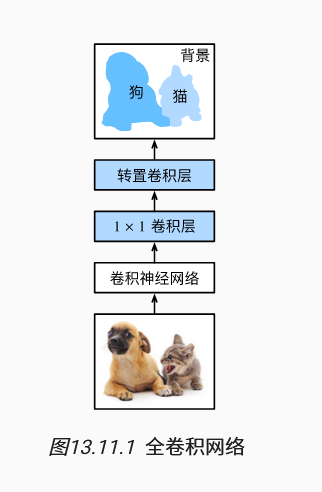
全卷积网络：用于实例分割。全卷积网络模型最基本的设计。全卷积网络先使用卷积神经网络抽取图像特征，然后通过卷积层将通道数变换为类别个数，最后通过转置卷积层将特征图的高和宽变换为输入图像的尺寸。 因此，模型输出与输入图像的高和宽相同，且最终输出通道包含了该空间位置像素的类别预测。

在图像处理中，有时需要将图像放大，即上采样，此时利用转置卷积实现双线性差值法。即初始化卷积核内部参数。

# 双线性插值法
def bilinear_kernel(in_channels, out_channels, kernel_size):
    factor = (kernel_size + 1) // 2
    if kernel_size % 2 == 1:
        center = factor - 1
    else:
        center = factor - 0.5
    og = (torch.arange(kernel_size).reshape(-1, 1),
          torch.arange(kernel_size).reshape(1, -1))
    filt = (1 - torch.abs(og[0] - center) / factor) * \
           (1 - torch.abs(og[1] - center) / factor)
    weight = torch.zeros((in_channels, out_channels,
                          kernel_size, kernel_size))
    weight[range(in_channels), range(out_channels), :, :] = filt
    return weight

2. 目标检测

2.1 标注位置

四元组标记一个矩形框，可以使用左上右下的x,y或者中心的x,y和长宽，这两种表示来表达一个矩形框在图像内的位置。

2.2 锚框法

目标检测算法通常会在输入图像中采样大量的区域，然后判断这些区域中是否包含我们感兴趣的目标，并调整区域边界从而更准确地预测目标的真实边界框（ground-truth bounding box）。 不同的模型使用的区域采样方法可能不同。 这里我们介绍其中的一种方法：以每个像素为中心，生成多个缩放比和宽高比（aspect ratio）不同的边界框。 这些边界框被称为锚框（anchor box）

我们以每一个像素点为中心生成多个锚框，生成规则如下：

最后得到图像高度,图像宽度,以同一像素为中心的锚框的数量,4的四维张量。

2.3 交并比（IoU）

我们需要衡量真实边界框与锚框之间的相似度，使用杰卡德系数，等于交集大小除以他们并集的大小。

• 我们以图像的每个像素为中心生成不同形状的锚框。
• 交并比（IoU）也被称为杰卡德系数，用于衡量两个边界框的相似性。它是相交面积与相并面积的比率。
• 在训练集中，我们需要给每个锚框两种类型的标签。一个是与锚框中目标检测的类别，另一个是锚框真实相对于边界框的偏移量。
• 预测期间可以使用非极大值抑制（NMS）来移除类似的预测边界框，从而简化输出。

要解决的问题，每个像素点生成锚框，则锚框过多。

十四. 自然语言处理

1.Word2Vec

1.1 跳元模型

目标：对于每一个词，学习到其中心词词向量和上下文词向量，最后该词的词向量一般由中心词词向量表示。

跳元模型假设一个词可以用来在文本序列中生成其周围的单词。假设上下文词是在给定中心词的情况下独立生成的（即条件独立性）。下述两公式相等：

$$P(\textrm{"the"},\textrm{"man"},\textrm{"his"},\textrm{"son"}\mid\textrm{"loves"}) = P(\textrm{"the"}\mid\textrm{"loves"})\cdot P(\textrm{"man"}\mid\textrm{"loves"})\cdot P(\textrm{"his"}\mid\textrm{"loves"})\cdot P(\textrm{"son"}\mid\textrm{"loves"}).$$

对于其中每一项，即在中心词为loves的条件下生成the的条件概率，我们通过对向量点积的softmax操作来建模，$u$为上下文词向量，$v$为中心词向量。注意这是一种自定义的简化方法。

$$P(w_o \mid w_c) = \frac{\text{exp}(\mathbf{u}_o^\top \mathbf{v}_c)}{ \sum_{i \in \mathcal{V}} \text{exp}(\mathbf{u}_i^\top \mathbf{v}_c)},$$

对于一个文本序列，定义总条件概率如下：

$$\prod_{t=1}^{T} \prod_{-m \leq j \leq m,\ j \neq 0} P(w^{(t+j)} \mid w^{(t)}),$$

训练时最小化负对数（一种乘转加的转化思想），即：

$$- \sum_{t=1}^{T} \sum_{-m \leq j \leq m,\ j \neq 0} \text{log}\, P(w^{(t+j)} \mid w^{(t)}).$$

1.2 连续词袋（CBOW）模型

连续词袋模型类似于跳元模型，其假设中心词是基于其在文本序列中的周围上下文词生成的。由于连续词袋模型中存在多个上下文词，因此在计算条件概率时对这些上下文词向量进行平均，最后通常使用上下文词向量作为该词的词向量。

NLP后续章节部分并未完全学习完，这是作者当时沉迷CV导致的。即使站在如今的眼光来看大多词编码方式都已经淘汰，但了解梳理清NLP方向的发展脉络仍然有助于我们继续创新，故本篇读书报告有待后续继续整理完篇~