『面向对象』面向对象第一单元总结——表达式求解
『面向对象』面向对象第一单元总结——表达式求解
一.前言
第一单元的主题是表达式解析与计算,主要学习目标是让我们这些OO小白初步了解体会面向对象层次化编程的思想,并浅浅进行代码上的实践(给大伙一..小小的OO震撼),把握不同类的拆分与继承,同时把握每一个类的属性,方法的设计,使得各个类间关系得当,构造出以类为基础的模块结构,并在主函数中用较短的代码(因为主要的代码实现应在类中)合理调度各个对象,实现最终要求。
本博客将分四个方面进行总结:度量分析,架构设计体验,自我Bug分析与找院友Bug方法,心得体会,接下来让我们一同走进美丽的OO世界。
二.度量分析
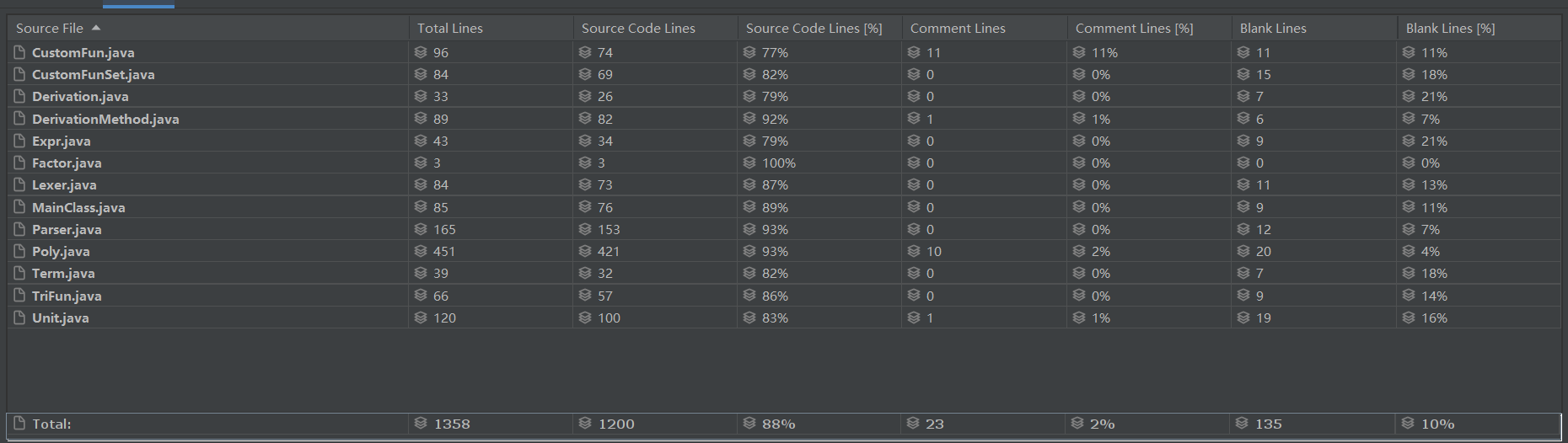
1.代码统计
本单元最终统计代码量1300+行,包含部分注释与辅助函数,去除后整体代码量在1200行左右,与整个项目的难度预期相符。除Poly类外大多控制在100行内,较为符合单一职责原则;而Poly类内存在大量化简函数与计算函数,长度来到400+行。
2.UML类图分析
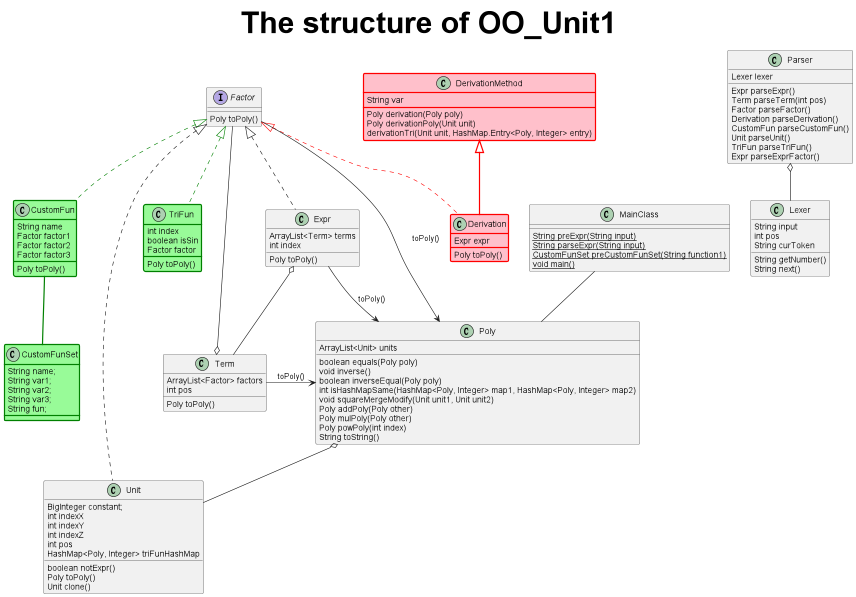
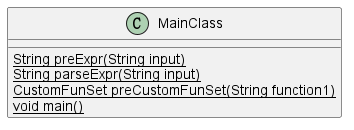
本单元历经三次迭代,最终UML类图如下,白色部分为第一次作业,绿色部分为第二次作业新增,红色部分为第三次作业新增。
可以看到,本结构以Factor,Unit,Poly类的实现为核心,在后两次的迭代中仅是增加对应类以及其余类的方法,并未进行大规模代码改动,很好的符合了开放封闭原则,展现出了极强的可扩展性,尤其是第三次作业,笔者基于此良好的架构,两个小时便完成速通。
然而本架构仍存在不足之处,点名批评Poly类,可以看到其函数过多,其功能过于冗杂繁琐,笔者认为或许应当像第三次作业构造了求导方法类一样,考虑构建一化简计算工具类来存储这些函数,使整体结构更为独立与美观。
3.复杂度分析
度量标准:
OCavg:平均操作复杂度
OCmax:最大操作复杂度
WMC:加权方法复杂度
CogC:认知复杂度
ev(G):基本圈复杂度,描述非结构化程度
iv(G):设计复杂度,描述模块耦合度
v(G):圈复杂度,描述独立路径的数目
以上笔者也是头一次听说,并且对其的概念仅限于数越大越复杂越不太好。
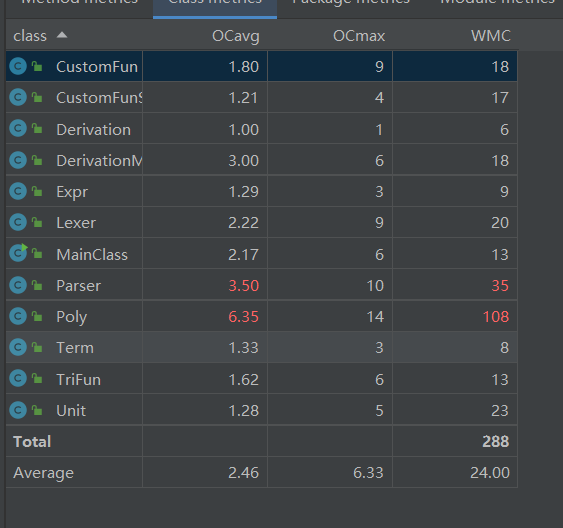
类复杂度:
由图可见,Parser类的平均复杂度与加权复杂度较高,而Poly类极高。这是由于Parser类主要负责对于表达式的解析,本次作业中表达式,三角函数,自定义函数等因子皆支持嵌套构造,因此解析过程中不可避免的会反复递归调用解析函数,复杂度必然较高。而Poly类是由于实现第二单元引入的三角函数化简所致,笔者完成了基本化简外又化简了平方和,诱导公式,而这些化简步骤皆在该类内实现,因此复杂度极高,具体原因下文说明。
方法复杂度:
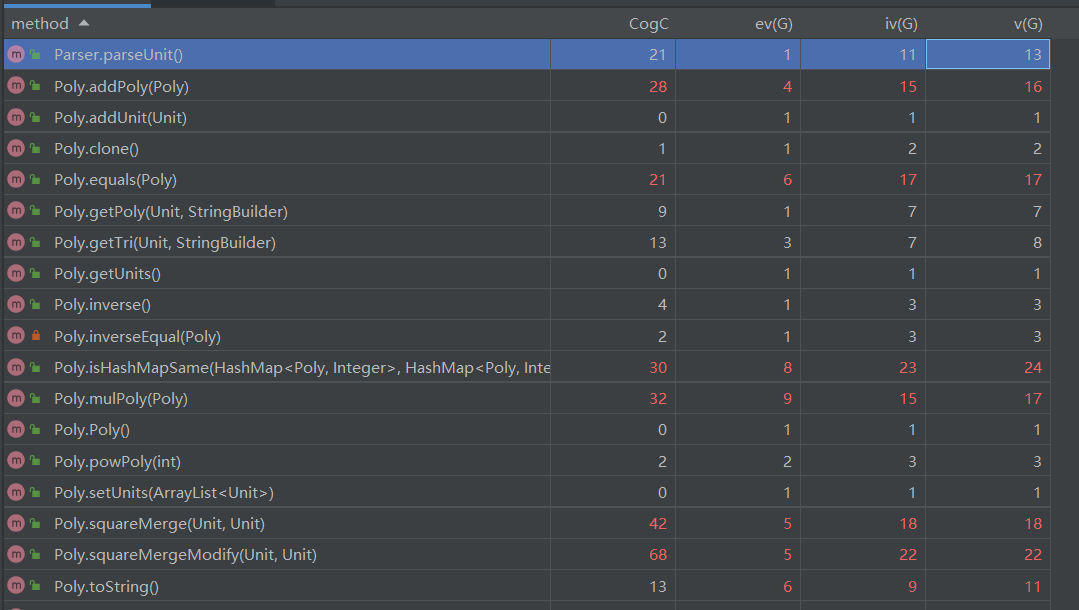
(1)Poly类:
一片惨淡的红~该类复杂度极高便不奇怪了。
首先是重写的equals函数,其用于判断两个Poly是否相等,以及isHashMapSame函数,其用于判断两个HashMap\
接着是addPoly和mulPoly方法,用于多项式的加法与乘法,要反复调用上述两函数的同时自身也要进行双循环遍历,因此复杂度极高。
squareMerge方法用于两个Unit的平方和化简,在addPoly中调用,其本质即一边找到sin(x)方而另一边找到cos(x)方并判断其余部分是否相等(支持常数不相等),相等即化简,因此同样需要双循环并调用isHashMapSame方法,复杂度同样极高。
(2)其余类:
CustomFun,TriFun内的toPoly方法,Lexer内的next方法复杂度较高,原因在于存在大量if-else语句以及存在遍历与递归的过程。
可见存在双循环乃至更多,以及大量递归调用的函数复杂度偏高,也许可以找到更加合适的算法优化函数降低复杂度。
三.架构设计体验
第一次作业发布伊始,笔者甚是迷茫,架构从何搭起更是无从下手,经历一天的冥思苦想后决定进行一个借的鉴,而发现了单项式多项式的思路后,顿时茅塞顿开,并在其中加入了大量自己的想法。在几次迭代中始终保持此架构,且增加功能愈发熟练。
根据BNF文法,一个表达式大致能拆成如下的架构:
表达式➡项➡因子(各种类型)➡递归…➡常变量
它是一个递归的过程,可以使用递归下降法层层解析,直到将表达式拆成数个最小单元,也就是常量与变量。
1.计算架构设计
在第一次作业中,我们可以将常量和变量全都看成一个基元,也可以称作单项式,即$pos \ constant \times x^{index_x} \times y^{index_y} \times z^{index_z}$。它由pos,constant,index_x,index_y,index_z五个属性构成,是一个广义的最小单位,这么做的好处是,不仅常量因子(变量的指数为0)和变量因子(常数项为1)可以统一由基元表示以外,连常量,变量,多项式彼此数学运算后得到的多项式也可以由多个基元构成,而且此种表示非常利于进行同类项的合并,因此我们可以想象到,无论是表达式,还是项,还是因子,都是由有限个基元构成,这为我们表达式的计算奠定了基础。
而第二次作业新增了三角函数,以上概念明显不再可行,但就如何存储一个“基本单位”而言仍能发现有相通之处。笔者将每一个基元新增一个HashMap<Poly, Integer>属性,其中HashMap中每一个键值对代表着一个三角函数因子, Poly存储的是该三角函数中含有的因子toPoly后的多项式Poly形式,Integer存储的是该三角函数因子的指数,同时令正数为sin,负数为cos,这点很有创造性,使用一个HashMap即可存储任何形式的三角函数,而通过这一键值对即可完全描述出一个三角函数因子。
Poly内存有ArrayList<Unit>,事实上无论是Unit自身,还是其余每种因子和项,都可以看作是一个Poly,而在类中皆提供了toPoly方法以便将当前层次及以下的所有内容转化成Poly形式返回,在实现上只需对顶层表达式toPoly,便会依次递归调用各层的toPoly,并自下而上层层计算返回,得到最终结果
2.解析架构设计
本次笔者与大多数人无异,采用的是递归下降法解析,根据文法对表达式有规则的解读,并根据读取到的特定token进入到不同的解析函数中,由于后两次迭代主要是添加不同因子,因此仅在parseFactor方法内调用了新增的parseTriFun,parseDerivation,parseCustomFun即可完成解析。
3.各类的设计考虑
(1)MainClass
主类实现自定义函数与待求表达式的输入,对于所有表达式的预处理与构造解析器进行解析,将自定义函数拆解存入CustomFunSet类,以及最后输出结果。
(2)Lexer
词法器类实现语法单元的顺序按步读取,耦合进Parser类中。
(3)Parser
语法解析器类实现对于表达式的解析,生成一颗层次结构分明的表达式树。
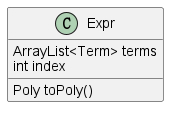
(4)Expr
表达式类实现Factor接口,存储表达式以及表达式因子,由ArrayList\
(5)Term
项类存储项单元,由ArrayList\
(6)Factor
接口类,本架构的精髓之处,所有种类的因子均实现此接口并重写toPoly方法,在存储时也均当作Factor对象统一存储,是里氏替换原则的最好体现。
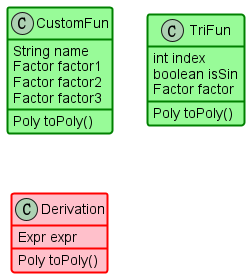
(7)TriFun, CustomFun(第二次作业),Derivation(第三次作业)
三角函数,自定义函数,求导函数因子,均实现了Factor接口,内部存储了描述对应因子的完备信息。
(8)CustomFunSet
自定义函数定义类,存储了自定义函数定义的相关信息,包括函数名,变量名,表达式,属于工具人类。
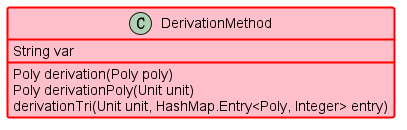
(9)DerivationMethod
求导方法类,Derivation继承了该类,该类属于工具类,提供Poly对变量var的求偏导方法,现在再来想想将该类合并进Derivation类也有道理。
(10)Unit
基元类,该类是核心类,有两个重要功能。由于在架构上笔者去除了独立的Num类和Var类,直接使用Unit类存储常量与变量,因此功能其一是作为因子实现Factor接口,而其二是作为基本单元存储基本项,所谓基本项即是由若干常量变量以及三角函数相乘得到。
(11)Poly
多项式类,由ArrayList\
四.自我Bug分析与找院友Bug方法
由于搭建了评测机进行了详尽的测试(Bug在测试里出麻了),在三次强测与互测中,笔者均未出现Bug,而互测中笔者秉持人不犯我我不犯人的和平主义者思想,仅浅浅出刀五次刀中五次。
若问为何准确率那么高,因为哥们采用了评测机硬测的方法,说来惭愧并未细细品读房友的代码,但在一长段表达式中一点点截取出房友出Bug的地方的过程中也明白了一些易错的点,与本单元自己犯下的错结合,一并与大家分享。
- 存常数时要使用BigInteger,因为题目中并无常数范围
- 注意自定义函数形参实参替换时左右加上”()”来保证运算顺序不变。
- 若化简了$sin(0)$,请注意 $sin(0)^0$ 的问题,或者说注意三角函数指数是0的问题,我出的两刀都来源于这个Bug。
- 遇事不决深克隆 深克隆很关键,避免破坏原有结构时应使用深克隆,对HashMap进行增删操作时应使用迭代器遍历。
- 不要过度优化 过度优化将会给你带来意想不到的错误(来自一位朋友的惨烈教训),圈复杂度越高出Bug的概率应当越高。
五.评测机搭建
本次作业的高效准确的完成离不开评测姬的鼎力支持,同时每个单元对于评测机的迭代开发也成了一个不简单的”作业”,甚至在第三次作业时搭评测机的时间超过了完成作业的时间。
简要来说,评测机是使用Python搭建,根据提供的文法为每一个结构(例如空格,符号,各种因子等)使用随机数随机生成的方法对其结构进行生成,并最后生成一个符合文法的字符串,将其传给python利用从事数学计算的Sympy包进行表达式运算同时传给我们所写的程序,python会通过代数值验算的方法比较二者是否相等,进而完成评测。换句话说,我们的程序便是完成了一个玩具版的Sympy。
我们需要将所有代码打包成JAR格式的工件,在Python中配置好参数并传入,完成Python到Java的沟通,具体操作请参考笔者未来也许会上传的源码。
六.心得体会
在略带微凉的初春悄然降临时,第一单元也迎来了尾声。历经三次代码的迭代训练,两次研讨课,两次实验课,以及最后的一篇总结,笔者在这万里长征的第一步中窥探到了面向对象的魅力。老师以及指导书的讲解,两次实验课代码精巧的结构设计,加以自己动手coding的课程作业向我们展现了面向对象层次化程序设计的优雅,并企图教会我们这一深邃的思想。第二次研讨课上伙伴们细致讨论了OO的五大核心原则,即S(单一责任原则)O(开放封闭原则)L(里氏替换原则)I(接口分离原则)D(依赖倒置原则)原则,这对我启发很大,并一条一条的尝试往自己的代码中匹配,并加以反思写过的代码的不足与改进之处,这些在上文略有提及。
尽管笔者上学期上过OO先导课,尽管早就知道第一次作业是递归下降法解析表达式,尽管上学期第七次作业已经练习过递归下降法的实现,笔者在真正拿到第一单元的指导书并研究一个小时后,仍是不免发出一阵叹息,并转身投入到第一单元训练的怀抱中去,后对着训练任务照猫画虎完成了解析表达式后,又为计算发了愁(实际第一次作业的计算有了思路后较为简单)。思前想后,笔者认为本单元的难点在于化简计算,并非是递归下降法的实现,依然记得第二次作业设计架构时的纠结,既想保留现有架构,又要容纳的下三角函数因子,想过用ArrayList,想过开两个HashMap表示sin&cos,想过HashMap里存Factor,从当初到如今思路的定型期间经历了无数次思考与尝试。相信大家有同感,本单元最难点在于三角函数的化简,不考虑花活的化简,其实完成基础的化简后,实现出平方和,诱导公式等花活也并非难事。笔者在第二周一整周几乎都在研究化简工作(并不完全为了卷性能分),边化简边生怕化出Bug,化简到神志不清,化简到后面一周都不想碰OO,功夫不负有心人,即使仍有一些化简不完全的Bug,但基本可以实现化简且并不影响正确性。当看到自己写的程序被大家挑不出毛病时,当和大家在侃侃而谈自己的设计实现思路时,当学到大开眼界的JAVA用法以及面向对象思想时,我想我收获到了来自OO这门课的快乐,也希望大家在每个单元的学习中不断提高境界,不断成长!
听说第二单元很多人边写边哭,边哭边写,已经迫不及待想被多线程电梯虐了捏(误。