『编译技术』SysY-Mips编译器设计——中端代码优化

章节目录

零. 前言

本部分任务为对LLVM中间代码做出代码优化，实际上大量的优化都集中于此。不要指望看这份文档就能看明白优化，因为笔者整理时也看不明白了。

一. Mem2Reg

0. 何为Mem2Reg？

在sysY中定义的变量称作原始变量，而在LLVM中的一个个变量我会称作虚拟变量(后续很有可能会统称为变量…但实际不一样)，定义和赋值的概念不再区分。

本优化不考虑全局变量和数组，仅针对单值int和指针(本质上是一字节的值)进行优化。我们最初的LLVM已经是SSA单赋值形式，而mem2reg这步，对于用LLVM为中间代码的我来说，应当是对原先的LLVM打散再重构的过程。

首先要明确，最初的LLVM是单赋值且单使用(除去Alloc指令)，一个原始变量被拆成过多的虚拟变量，因为我们使用的每一个原始变量都是从内存中LOAD取出，即一个虚拟变量被单赋值的同时也仅被使用了一次。

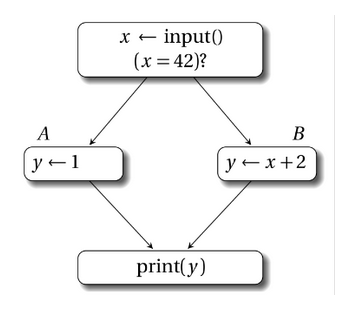
我们现在要依据每个原始变量的def-use链(一个变量的生命周期，从被定义，到被使用，到再次被定义结束) 改造成单赋值多使用的形式，同样是将原始变量拆成多个虚拟变量，但是仅在定义时拆。通过这第一步，我们便可以消去一部分的访存指令。但由此会引发一个重大的问题，借用教程的图图。

在分支汇总处，一个原始变量的取值会取决于数据从哪条分支上流入，上图AB块中的两个y我们称作y1和y2，print块中的y并非定义而是使用，那么它的取值便成了未知数，我们用y3 = phi [A, y1], [B, y2] 这条指令对y进行一次定义，y3成为此时y的唯一取值。

接下来的工作便是以基本块为最小单位找到插入phi指令的位置，进而找到哪些变量需要使用phi指令的返回值。核心目标是使得每一个原始变量在代码的任何地点有唯一的虚拟变量取值。

1. 计算基本块前驱与后继结点

依据基本块跳转指令来记录每一个基本块的前驱和后继基本块们就可以，记录基本块前驱与后继。进入节点无前驱，退出节点(最后一条为return语句的基本块)无后继。

2. 计算被支配节点（支配集合）

首先定义如下:

  1. 支配（dominate）：如果CFG（Control Flow Graph）中从起始节点到基本块y的所有路径都经过了基本块x，我们说x支配y，按照这个定义，每一个节点都支配自己。

  2. 严格支配(strict dominate)：如果x支配y，且x不等于y，那么x严格支配y。

  3. 直接支配者（immediate dominator, idom）：严格支配n，且不严格支配任何严格支配 n 的节点的节点(直观理解就是所有严格支配n的节点中离n最近的那一个)，我们称其为n的直接支配者。

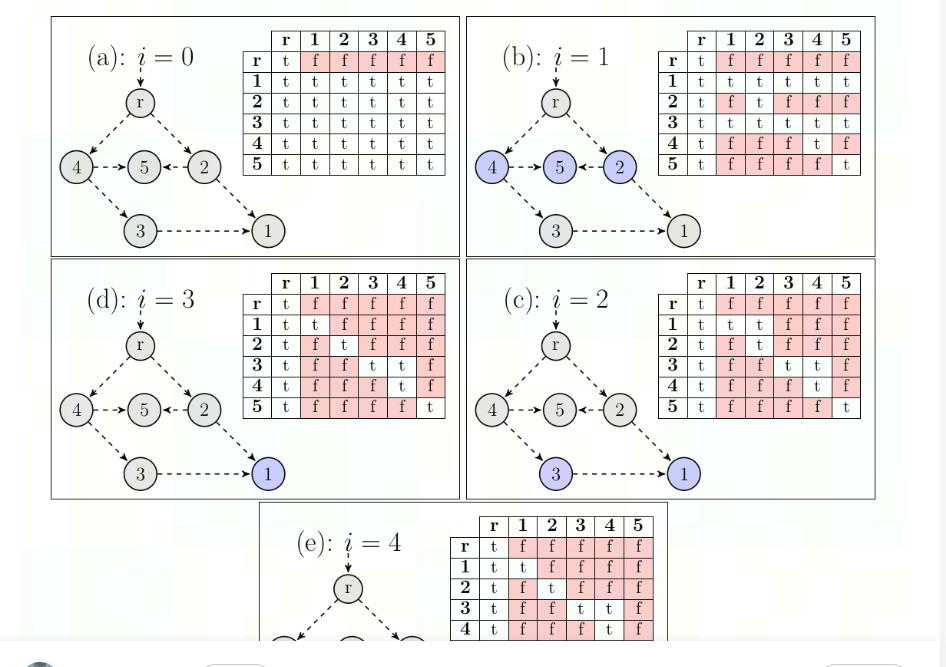
接下来我们计算每个节点被哪些节点支配。Lengauer-Tarjan算法较为复杂，我们采用迭代数据流算法，流程如下:

  1. 将起始节点设为r，初始化为仅被自己支配
  2. 其余起始支配节点初始化皆为被全部节点支配。每个基本块保存一个HashMap<BasicBlock, Boolean>用作记录被支配关系。
  3. 每次迭代取前驱结点的被支配集合的交集与自身的并，直至集合无变化，此时得到各节点支配关系，注意这不是支配树。

所谓a严格支配b，对符号x而言，即b中的第一次定义x之前的值完全由a的最后一次定义来决定，不存在任何歧义。因此显然自己无法严格支配自己。

3. 计算直接支配者

根据定义(严格支配n，且不严格支配任何严格支配 n 的节点的节点)计算，我们已经求得支配 n 结点的全部节点，只需要遍历一遍即可找到藏在其中的直接支配节点。

每个节点的直接支配者是其父节点，根据此关系我们构造出了支配树。

4. 计算支配边界

首先明确为何计算支配边界，一个节点的支配边界代表着支配范围的边界，在该节点对变量的定义会在边界处会产生歧义(即这个定义只是多个取值的可能一种取值)，因此我们需要计算支配边界来找到插phi的位置。

我们已经求得每个节点的直接支配者，采用如图算法。

img_1.png

简单解释该算法，我们遍历有向图中每一条边(a指向b)，从两个节点最近的位置，即一条边开始，逐渐沿a的直接支配者往上，直至a能够直接支配b，在此之前的遍历到的所有节点，其支配边界都该包含b。

注意，自己可以是自己的支配边界，考虑 0 --> 1 --> 2 --> 1，即出现回边时，自己基本块的定义也可能不由自己决定。

5. 插入phi节点

核心算法如图：我们得到了支配边界后，此时以原始变量作为最小单位，记录下原始变量在哪些基本块中被定义过(此时需要与符号表配合，见改造符号表一节)，进而找到基本块集合的支配边界，由于我们要在支配边界上插入定义的phi指令，支配边界也便成了定义的基本块，因此需要将支配边界也纳入基本块集合中，同时记录支配边界们，直至找到闭包，定义基本块集合不再变化。

这时我们求得了待插phi的支配边界集合，但是要明确的是，经过上述算法得到的是可能插入phi的位置，并非一定插入，由于我们的文法支持各处定义，在一个基本块插入phi值时可能出现该变量未被定义的情况，这是不应该的，因此在得到插入phi的基本块集合后，需再次判断该变量在该基本块是否存在定义。这一条限制是我们SysY文法的限制，而非一般算法中给出。

在重命名前，即使Phi指令未被填全，但是该指令的Value(即该变量在基本块中的新定义)已然存在。新增的Phi填充完毕，意味着此时变量定义已然完备，一个变量在任何位置都具备了变量唯一性，重命名只需要做两件事，计算Phi指令流入的Value，为一开始找不到定义的假标签找到属于它的Value。

证明：插入phi后，若在当前基本块x仍找不到定义，则其真正的定义一定在直接支配者y中：

当前基本块找不到定义，说明当前基本块未定义，且未插phi，说明该基本块未被当作支配边界，则该基本块定义唯一来自其直接支配者y。

6. 重命名phi

我们由第三步可得知节点的父节点，根据父节点推出每个节点的子节点，构建支配树，为接下来DFS做准备。

我们需要DFS支配树，基本块a是基本块b的直接支配者并不意味着基本块b中的变量由a中的变量直接决定，而是由a中的变量和将b作为支配边界的基本块们中的变量共同决定。

重命名需要三步：

  1. 需要判断当前插入的phi的合理性，即是否沿每条前驱块都能找到对应定义；
  2. 为phi指令的每一条数据流找到归属；
  3. 重命名该基本块内在生成phi之前无法得到准确赋值的被使用的变量。

为phi值添加基本块流，需要保证其每一个前驱基本块都要为phi提供一条数据流，对于每一前驱块，沿其直接支配者找到最近的该原始变量定义，将其填入phi指令中。这一步的正确性基于DFS支配树，保证遍历到一节点时，其直接支配者的phi指令都已装配完毕。

重命名假标签同理，首先判断在Phi指令的插入后能否在当前基本块找到定义，若找到则重命名假标签为该phi值；若找不到，则沿其直接支配者找到最近的定义即可。

上述寻找过程一定都能找到，因为在插入PHI以后，已经确保了每个原始变量在每一时刻的虚拟变量的唯一性。

1
2
3
4
5
6
7
int main(){
    int a1 = 1;
    if (a1 > 3) {
        a1 = a1 + 3;
    }
    return 0;
}

考虑如上情况a1应该被唯一确定，if内a1并非处在a1的决策边界处，DFS支配树。

img_10.png

给出官方的算法，由于本人到这一步看不太明白，因此上文均是自己推导，经评测验证应为正确。

二. 基本块合并

这一步应用在CFG之后，计算支配关系之前，因为涉及到对基本块的删除，主要工作有二：

  1. 将非连通基本块删除
  2. 将相邻基本块(该基本块有且只有一个前驱且该前驱有且只有当前基本块一个后继)和二为一，指令相融合

由于我们在上文已把基本块的关系构建完毕，接下来处理较为容易，有两点需要注意：

  • 基本块间的关系是一个双向链表，在合并以及删除时应注意前驱节点和后继节点的修正。

    具体来说，设被合并删除的基本块为a，合并的基本块为b，则a不再是b唯一的后继节点，而a的后继节点成为b新的后继节点；a的后继节点们的前驱节点也不再是a，而替换为b!

  • 合并基本块会导致定义位置紊乱，可能无法沿支配树找到最近Value，需要额外的操作。

    • 我们可以遍历被合并的块全部指令，用合并块的定义表进行匹配，将能匹配上的假标签替换为合并的块的定义Value，由于存在先后关系，定义表中保存的变量定义是最后一次定义，而被合并块存在的假标签一定是在该基本块第一次定义之前出现的，因此匹配正确性得到保证。
    • 将被合并块的定义符号表(IrSymbolTable)转移到合并块的定义符号表，若合并块中存在该变量定义，则替换(因为被合并块的在合并块之后)；若不存在，则加入。

三. 死代码删除

1. 概念：

程序包含的一些代码可能并不会被运行或者不会对结果产生影响，那么我们称这种代码为死代码。我们将不会被运行到的称为不可达代码，将不会对结果产生影响的代码成为无用代码。删除无用或不可达代码可以缩减IR代码，可使程序更小、编译更快、执行也更快。

2. 死函数删除

构造函数调用链，删除没有使用过的函数。不过这一步只能减少生成的代码，并不会减少执行的cycle。使用BFS计算出有价值函数的闭包，其余删除。

3. 死代码删除

我们目前认为的有价值指令有：br, ret, call, store（有待商榷，需要进一步做内存分析，全局变量的store可以无脑加，局部变量的store取决于后续有无使用它的，需要涉及到公众子表达式删除等问题），其中store会在后文进一步优化。

采用逆推的形式，将所有有价值指令标记，再将有价值指令的操作数标记，大体思路同死函数删除，使用BFS计算出有价值指令闭包，其余指令删除。

四. 局部公共子表达式删除

局部子表达式删除的正确性建立在基本块内指令的顺序执行。若是在全局范围内优化，则需要考量基本块执行顺序的问题，出现哈希冲突时并不代表其中存在可以优化的项，例如在两个分支中出现了

分支1：c1 = a + b, d1 = c1 + a；
分支2：c2 = a + b, d2 = c2 + a；

此时我们不能将c2优化为c1，因为c1在这条分支中不会被计算。我们针对部分指令进行局部子表达式删除，包含add,sub,mul,div,getelementptr,cmp。该优化以每条指令为最小单元，站在基本块视角进行，步骤如下：

  1. 对于每个BasicBlock初始化一个哈希表
  2. 对每条指令，获取它的操作数和操作符，根据操作数和操作符计算哈希值，需要特别考虑add，mul，cmp三类指令，他们存在着多种等价形式，add和mul将操作数颠倒同样等价，而cmp需要考虑的更多，例如a>b和b<a等价。
  3. 扫描基本块内全部指令，计算哈希值，如果哈希表中已经存在该值，那么我们直接将BasicBlock里后续用到该Value的地方全部替换为哈希表内存的Value，否则将哈希值及对应的Value存入哈希表

五. 常量折叠与传播

  • 提前计算好操作数为常数的表达式，针对add,sub,mul,div,cmp等进行了常量折叠，缩减计算指令。

  • 只进行了较为简单的复杂折叠，诸如 0 * a, 1 * a, 0 + a, a - 0, 0 / a 等相邻情况的简单优化。

六. 优化Store

有时我们会在load之前多次对同一个地址进行store，那么显然只有最后一个store是有效的，前面的store指令可删除。因此我们可进行内存分析，删除一些无用的store指令，注意删除后可能会暴露新的优化空间，需要再次进行死代码删除。

七. 全局指令移动（超简化版）

指令移动时有如下要求：

  1. 操作数在循环中不变，为定值。
  2. 移动不会产生副作用：比如涉及存入内存等指令，若提出循环外，则可能没进循环，却由于外提而执行这条指令导致影响下文，这种即产生了副作用。
  3. 为变量赋值也是一种会产生副作用的操作，经过了死代码删除后，留下的被赋值的变量一定会在下文中被用到，外提还需要对phi指令做一些处理，比如循环外对i赋值，循环内也对i赋值(但满足操作数不变)，此时在循环结束后使用i值，正常应该是使用phi将两个数据流汇总，而外提后存在一些问题。

我们首先通过深度优先遍历CFG找回边得到处于循环内的基本块，我们只针对循环内的基本块中某些语句做出前提，一是由于循环外指令再怎么前提也不会产生正面优化，二是指令前提也会产生活跃变量范围增大，溢出节点增多等副作用，需要权衡考虑。

为简单起见，我们只将偏移量为常数的gpr(getElementPtr)指令尝试前移至基地址的定义位置之后，若使用全局变量基地址则前移至入口基本块处，如此可避免多次重复计算访存地址。

正确性证明：一是gpr内操作数不变，二是gpr的结果并非是原始变量，而是临时变量，不会对phi流产生影响，一定不会存在副作用。

经实际检验，简化版的指令移动在第七个竞速测试点已经得到了大量优化！同时可以肯定地说，这部分优化非常关键，是做完Mem2Reg后提升性能的关键！