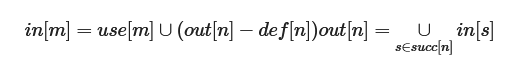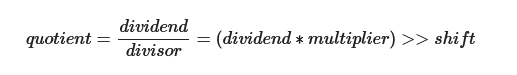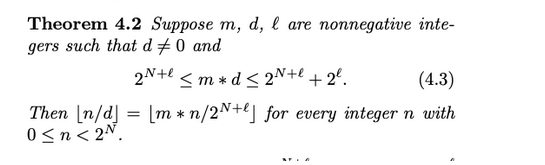『编译技术』SysY-Mips编译器设计——后端代码优化

章节目录

零. 前言

本部分任务为对Mips后端代码做出代码优化，主要是配合中端优化的后端消PHI和图着色寄存器分配。实际上，后端优化更多涉及特定的体系结构，这里实现的仅仅是冰山一角。

一. 后端消PHI

这一步说是优化，然而是LLVM经历过mem2reg优化后不得不做的一步。

消PHI即将PHI指令消去，换句话说，PHI指令的Value值应该保留，但后面的数据流应当通过Move指令消去。LLVM具备规则，对于基本块B，若其有多个前驱的基本块$B_{1}, B_{2}…$且$B$中存在phi指令，我们可以在$B_{i}\rightarrow B$之间添加新的基本块$B’$ ，新添加的基本块内只有一种指令，即move指令。

参照教程内思路，首先遍历全部基本块，找到入口存在phi指令基本块B(存在phi指令意味着其一定有两个及以上前驱节点)，遍历其每个前驱节点$B_i$，若其拥有超过一个后继节点，则$(B_{i}, B)$称作一对关键边，在这之间创建一新基本块$B’$，若$B_{i}$仅有$B$一个后继节点，则后续在$B_{i}$结尾进行。

创建好基本块后，遍历$B$中所有phi指令，对于 %x = phi((%b1 %v1), (...))，找到其前驱基本块b1对应的Move指令插入位置，可能是新基本块或基本块末尾，插入指令 %x = move %v1，对于phi内其他数据流同样操作即可。

如此我们通过加入大量move指令，完成了对LLVM的消PHI工作，在后续我们会尝试将move合并以缩减多余的move指令。

注：move是自己定义的假指令，对标mips里的move，其中保存两个Value记为target与source。

二. 图着色寄存器分配（核心）

mips优化中最核心的一步，经历消PHI后，我们便可以着手生成mips代码。生成时进行图着色寄存器分配优化。

在之前的阶段当中我们都假定了有无限个寄存器作为虚拟变量，而实际上mips后端的寄存器有限，经过大量摸索后寄存器分配如下：

zero, at不参与分配；
v0, v1用作机动寄存器，即使用后立即释放，不会引起任何冲突，用于承接立即数与在超过两个操作数的指令中进行中间计算，同时v1还被设置用来存放图着色后溢出的节点，并立即存入内存中，这两个寄存器不参与分配；
sp,fp,ra,gp寄存器用于维护堆栈，全局变量，返回地址等，不可分配；
a0~a3用作函数传前四个参数，不参与分配；

实际上，这四个寄存器有过考量，最终实践证明传参非常需要用来中间过渡的寄存器，否则由于传参寄存器冲突导致访存开销过大！
其余20个寄存器参与图着色寄存器分配。

1. 计算活跃变量

应用在课内学过的计算活跃变量的方法，我们以基本块为单位计算出每个基本块内全部指令in和out集。计算方法为一个基本块中由下至上由out倒推in，而基本块内最后一条指令的out集由其后继节点们第一条指令的in集的并集决定，如此迭代计算，直至每条指令的in和out集合不再变化。为减少迭代次数，可以考虑从出口节点开始遍历。如此我们计算出了多个活跃变量集合，也即是变量冲突的多个时刻。

具体而言针对每一条指令，in集等于out集加上该指令的操作数节点，再减去该指令节点，如下图算法所示：

2. 构造冲突图Build

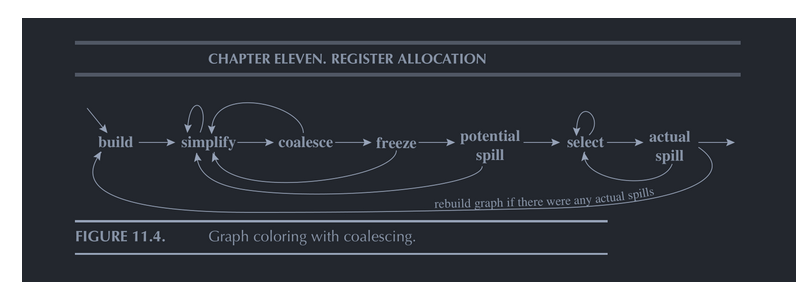
接下来开始图着色寄存器分配，整体算法如图所示：

一个活跃变量集合里包含的元素两两冲突，彼此间都会形成一条无向边，我们在Value类内记录每个节点的邻接矩阵，遍历所有的活跃变量集合，得到冲突图，同时需要记录下move指令的两个节点，在后续可尝试合并。

冲突图代表着节点之间的冲突关系，存在边的两节点无法共用同一寄存器，我们进行启发式的图着色算法来为每个节点分配寄存器，最终目的为在生成mips之前，每个虚拟变量被分配到了有且仅有一个唯一的寄存器。

3. 简化Simplify

我们删除冲突图中度数小于$K(20)$的点，简化冲突图，将其入栈，产生更多的图着色机会，因简化步骤而入栈的节点一定可以分配到寄存器。

4. 合并Coalesce

move指令的两端节点本质相同，可进行保守式的合并，若合并后的度数总和小于K，则进行合并, 即二节点共用同一寄存器，将被合并的点彻底移除冲突图(需要记录下合并的点，为后续分配寄存器时能够得到合并点分配的寄存器)，同时注意维护现有图的邻接边关系；若合并后总度数大于K，则我们不进行合并，因为合并后可能会产生新的溢出节点，得不偿失。

5. 冻结Freeze

反复执行简化和合并的步骤，直至图中节点无法改变。

6. 溢出Spill

无法合并与简化时，将度数大于等于K的结点标注为不可分配寄存器，然后从冲突图中去除，将其入栈，因溢出步骤而入栈的节点不一定能分配到寄存器。溢出节点后简化了冲突图，会暴露出更多的合并和简化机会，如此反复，直至冲突图为空。

7. 选择Select

当冲突图为空时，开始从栈中挨个取结点，重新生成冲突图，为在简化步骤时入栈的结点分配寄存器，将溢出步骤时入栈的结点置入不可分配的集合。

最后尝试将不可分配寄存器集合的结点取出尝试为其分配寄存器(由于move等原因可能存在为其分配寄存器的可能)，若当真无法分配，则进行标记，将其转化为活跃范围较小的变量，并进行重新开始。

8. 重新开始Restart

如果无法进行着色的集合不为空，那么则需要改写程序，为这些变量在内存当中分配空间，并且在每次使用需要将其从内存当中取出。

这一步骤是最关键的一步，也是笔者改造最多的一步，关键在于如何理解教程中这段话：

每次修改需要存进内存当中，这种情况下，溢出的临时变量会转变为几个活跃范围很小的新的临时变量，这个时候需要重新进行活跃分析、寄存器分配，直到没有溢出和简化为止（通常只需要迭代一两次）。

冲突图中的节点有两种可能，一种是指令节点，另一种是函数的形参节点，假设某节点是溢出的节点，意味着该节点应当在出现后立刻存入内存中，将其从活跃变量流中杀死，而使用到该变量节点时从对应地址中取出，再使用。

出现：若节点是函数形参，则在函数最开始便已经出现，因此也在函数最开始添加指令，若为前四个参数则将对应的A寄存器存入内存，若为后续形参，则我们会在调用函数时处理将形参存入内存的过程，而并非在函数头执行；若节点是指令节点，则在其被赋值的时刻出现，我们需要在下一条紧接Store指令，将其存入内存当中。

而为溢出节点分配寄存器本人采取了两种方式：

对溢出节点作标记后重新开始：该节点被使用时不再纳入活跃变量集合中，而与之绑定的store指令的操作数(也就是该溢出节点)仍需要纳入活跃变量集合，此时我们将该溢出节点活跃范围缩小，进而重新进行图着色分配，直至再无溢出节点。
将溢出节点寄存器设置为机动寄存器V1：由于溢出节点在store后寄存器会立刻释放，不如使用机动寄存器进行转存，如此确保一趟图着色便可分配完毕，避免了重新开始的步骤，最后采用第二种方法，正确性无误。

以下是coding时一些随笔：

从哪取：偏移量如何设置，偏移量来自两个地方，一个是数组的声明，一个是我们放不下的虚拟变量，先装我们的虚拟变量，翻译mips时实时填入二维数组。
全局变量该如何记录，需不需要应急寄存器，全局变量符号出现在Load(无需缓冲)和GTR处(涉及计算，需要缓冲)，使用V1作为缓冲即可。
最后每一个变量都会被分配一个绝对不会产生冲突的寄存器，生成Mips时直接对照寄存器无脑灌入即可。
问题：即使有限次迭代可以保证分配好寄存器，但仍然存在死循环的可能性，当一个变量V无法分配寄存器，而将其转换在前面load出来时，由于load也需要一个寄存器承接，因此即使V不作为活跃变量在寄存器内流向更前面的定义处，而在当前处(load的out)处仍存在冲突的可能性，这时需要重新开始。

9. 经过图着色寄存器分配后的结果

每一条指令Value 都唯一确定分配好了一个寄存器，而使用的Value除常数外有两种情况。

在寄存器里；
由于寄存器冲突而存在内存中，此时备注好了相对于FP的偏移，使用机动寄存器取出即可。

接下来按照指令类型翻译为mips即可，相较于优化前，这一步是轻松许多的！

10. 生成mips

整体较为eazy，有两个重点：

对溢出节点的处理：溢出节点的处理方式正是做优化前对于无寄存器可分配的Value的处理方式。秉持上述原则，在处理地址问题便没有歧义了。
对函数传参的处理：由于图着色后，形参和实参都分配好了寄存器，无可避免的会出现传递的当前形参的寄存器后续的实参还要用到，此时无法直接move的情况，此时需要一些算法来规避影响，最为简单的方法是用一块内存空间作为缓冲，实参先存入内存中，形参再从内存中调取。然而这会产生大量存取内存指令，违背了我们优化的初衷，因此这也是为何要令$A0~$A3作为传参缓冲寄存器的理由。